研究活動
1. プラズマ流体平衡・安定性グループ
|
プラズマ流体近似に基づく理論及び数値シミュレーションを駆使して、磁場閉じ込め核融合プラズマの平衡、安定性、非線型発展等における性質を解明することを目指します。LHDプラズマで観測される現象の物理的機構を明らかにすることを中心とした解析を行います。プラズマの自己安定化現象、崩壊現象、誤差磁場等による磁気島の影響、ペレット溶発現象等の解析を通じて、安定放電領域限界や最適な粒子補給手法に関する系統的な知見を得るための研究を行います。同時に、モデル方程式の拡張やそれに基づくコード開発を進め、それまでの解析結果の修正や新たな知見の獲得を目指します。さらに、これらの知見を基に、トロイダルプラズマ全体にわたる普遍的な学理の構築を目指し、輸送モデルや他の理論研究との関連も検討します。
|
 |
最近の研究成果
| 三次元平衡計算と電場計測との比較によるLHDプラズマの最外殻磁気面の同定 | ||
|
HINT2コードによるシミュレーションで得られた磁力線長が急激に短くなる位置と、LHD実験において計測された周辺電場シアが最大となる位置が良く一致し、この位置を最外殻磁気面の位置として同定することができた。
(Y. Suzuki et al 2013 Nucl. Fusion 53 073045.) |
||
磁力線ポアンカレマップと径電場シア 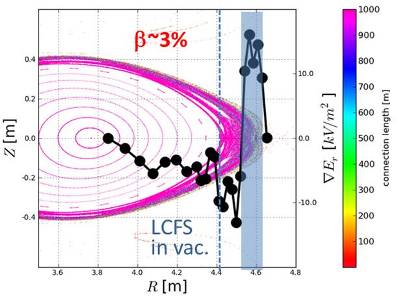 |
磁力線長と径電場シアの比較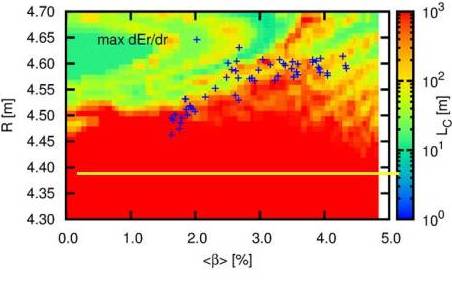 |
|
| RFPプラズマのヘリカル構造への非線型遷移の再現 | ||
|
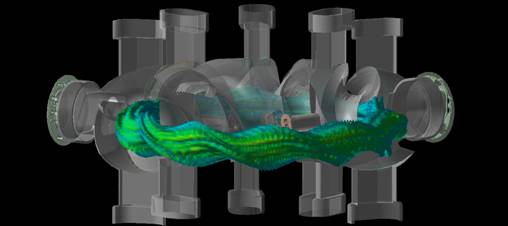
軸対称プラズマである逆磁場ピンチ装置(RFP)の実験において、プラズマが自発的にヘリカル構造に遷移することが観測されており、その状況を三次元MHDコードMIPSを用いた非線型MHDシミュレーションによって再現することに成功した。
(N.Mizuguchi et al., Plasma and Fusion Research 7 (2012) 2403117.)
|
||
初期平衡圧力分布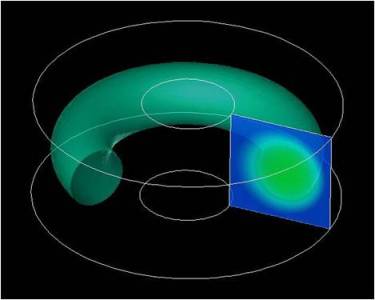 |
遷移後の圧力分布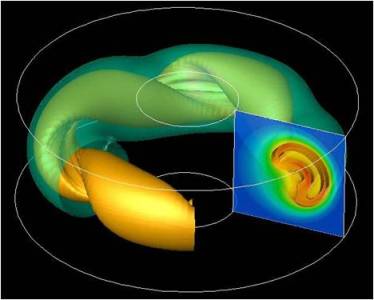 |
|
シミュレーションコードの紹介
|
名称:CAP
|
|
|
名称:MIPS
|
|
|
名称:HINT2
|
|
|
名称:NORM
|








 「NIFS」へ
「NIFS」へ